
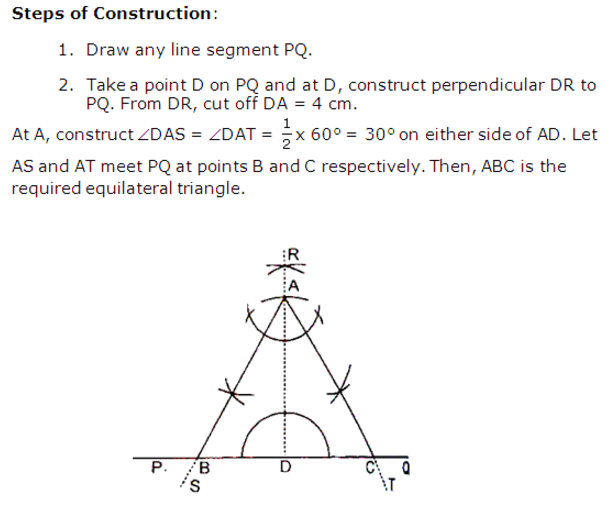
Construct a circle around O with radius (3/2)^(1/2) * OM. Construct the square's diagonals and let center of the square be O. Let two adjacent corners of it be M and N.
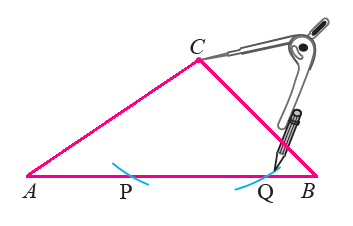
Construct a square with side length c first. Construct 3 more triangles congruent to the original triangle on the outside of each of the three other sides of the square in such a way that a larger square with side length a+b is formed. Construct square with side length c on the opposite side of c from the triangle. Consider any right triangle with hypotenuse c. We start with some observations in the first paragraph and describe the construction in the next paragraph. Join the vertices to get the required triangle. So, we draw and from it's midpoint, we draw a segment forming an angle We draw perpendicular on and denote the angle between the median and as. With this, we get a conclusion of this triangle should have a length ratio of. By solving this quadratic equation, we get, the length of the two sides would be and. By using Pythagoras Theorem, the length from the origin to this point is and the length from this point to the point (2,0) is. The desired point which have a horizontal length of from the origin would have a vertical length of when substituted into the previous equation. Let be the horizontal length from the origin to the desired point on the circumference which satisfies the question. Let the circle has an center of (1,0) on a Cartesian plane. The radius of the circle with the hypotenuse as the diameter will be 1. WLOG, let the length of the hypotenuse be 2. A angle is easily constructed by bisecting a angle (which is formed by constructing the altitude of an equilateral triangle), and angle is constructed by constructing a 15 degree angle on top of the 60 degree point. Thus, and, and so one of the angles of the triangle must be and the other must be. Because as well, we immediately deduce via some short computations through quadratic formula that and. Indeed, we notice that the altitude of the triangle is of length, which both of the solutions set equal to. It is not difficult to reconcile these two constructions. However, since, we can rewrite the condition asįrom this it becomes apparent that or hence the other two angles in the triangle must be and, which are not difficult to construct. Therefore if we construct a circle with diameter and a line parallel to and of distance from, either point of intersection between the line and the circle will provide a suitable third vertex for the triangle. However, twice the area of the triangle is also the product of and the altitude to. However, we notice that twice the area of the triangle is, since and form a right angle. The conditions of the problem require that (This is true because if we inscribe the triangle in a circle, the hypotenuse is the diameter, so a segment from any point on the circle to the midpoint of the hypotenuse is a radius.)
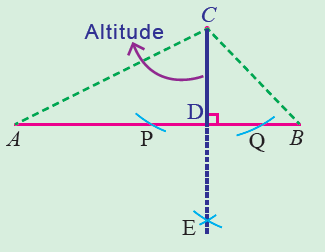
We also observe the well-known fact that in a right triangle, the median to the hypotenuse is of half the length of the hypotenuse. We denote the catheti of the triangle as and. Construct a right triangle with a given hypotenuse such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.


 0 kommentar(er)
0 kommentar(er)
